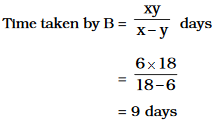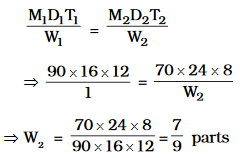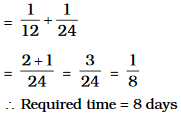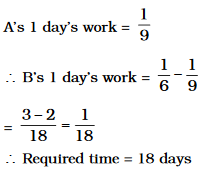Practice Time and Work

1 / 20

A can do a work in \[10\] days and B in \[15\] days. How many days will both take together to complete the work?

\[2\] days

\[4\] days

\[6\] days

\[8\] days

Combined work by \[(A+B)\] in \[1\] day

\[=\frac{1}{\left(A's\ 1\ day's\ work\right)}+\frac{1}{\left(B's\ 1\ day's\ work\right)}\]

\[=\frac{1}{10}+\frac{1}{15}\]

\[=\frac{3+2}{30}\]

\[=\frac{5}{30}\]

\[=\frac{1}{6}\]

\[\therefore\] A and B will complete the work in \[6\] days.

2 / 20

Prev Next

A can do a work in \[10\] days, B in \[15\] days, and C in \[30\] days. How many days will they take together to complete the work?

\[2\] days

\[3\] days

\[4\] days

\[5\] days

Combined work by \[(A+B+C)\] in \[1\] day

\[=\frac{1}{\left(A's\ 1\ day's\ work\right)}+\frac{1}{\left(B's\ 1\ day's\ work\right)}+\frac{1}{\left(C's\ 1\ day's\ work\right)}\]

\[=\frac{1}{10}+\frac{1}{15}+\frac{1}{30}\]

\[=\frac{6+4+2}{60}\]

\[=\frac{12}{60}\]

\[=\frac{1}{5}\]

\[\therefore\] A, B, and C will complete the work in \[5\] days.

3 / 20

Prev Next

A alone can complete a work in \[12\] days. A and B together can complete it in \[8\] days. How long will B alone take to complete the work ?

\[16\] days

\[20\] days

\[24\] days

\[28\] days

\[A's\ 1\ day's\ work=\frac{1}{12}\]

\[(A+B)'\ s\ 1\ day's\ work=\frac{1}{8}\]

\[\therefore B's\ 1\ day's\ work\]

\[=\frac{1}{8}-\frac{1}{12}\]

\[=\frac{3-2}{24}\]

\[=\frac{1}{24}\]

\[\therefore \ B\ alone\ can\ do\ the\ work\ in\ 24\ days.\]

4 / 20

Prev Next

A and B can do a work in \[12\] days, B and C in \[15\] days and C and A in \[20\] days. If A, B and C work together, they will complete the work in :

\[4\] days

\[6\] days

\[8\] days

\[10\] days

5 / 20

Prev Next

A can do a work in \[6\] days and B in \[9\] days. How many days will both take together to complete the work?

\[2.5\] days

\[3.6\] days

\[4.8\] days

\[5.2\] days

6 / 20

Prev Next

A can do a piece of work in \[20\] days and B can do the same piece of work in \[30\] days. Find in how many days both can do the work ?

\[10\] days

\[12\] days

\[14\] days

\[16\] days

7 / 20

Prev Next

A and B together can do a piece of work in \[6\] days. If A can alone do the work in \[18\] days, then the number of days required for B to finish the work is

\[7\] days

\[9\] days

\[11\] days

\[13\] days

8 / 20

Prev Next

A’s \[2\] days’ work is equal to B’s \[3\] days’ work. If A can complete the work in \[8\] days then to complete the work B will take

\[10\] days

\[11\] days

\[12\] days

\[13\] days

A’s \[2\] days’ work = B’s \[3\] days’ work

\[\therefore\] Time taken by A = \[8\] days

\[\therefore\] Time taken by B \[= \frac{8}{2}\times3\]

\[= 12\] days

9 / 20

Prev Next

If \[90\] men can do a certain job in \[16\] days, working \[12\] hours per day, then the part of that work which can be completed by \[70\] men in \[24\] days, working \[8\] hours per day is

\[\frac{1}{2}\]

\[\frac{3}{4}\]

\[\frac{5}{6}\]

\[\frac{7}{9}\]

10 / 20

Prev Next

A and B can do a piece of work in \[15\] days. B and C can do the same work in \[10\] days and A and C can do the same in \[12\] days. Time taken by A, B and C together to do the job is

\[2\] days

\[4\] days

\[6\] days

\[8\] days

11 / 20

Prev Next

A can do a piece of work in \[12\] days and B in \[24\] days. If they work together, in how many days will they finish the work?

\[6\] days

\[8\] days

\[10\] days

\[12\] days

(A + B)’s 1 day’s work

12 / 20

Prev Next

A and B together can do a piece of work in \[6\] days and A alone can do it in \[9\] days. The number of days B will take to do it alone is

\[10\] days

\[14\] days

\[18\] days

\[20\] days

(A + B)’s 1 day’s work = \frac{1}{6}

13 / 20

Prev Next

A and B together can do a piece of work in \[9\] days. If A does thrice the work of B in a given time, the time A alone will take to finish the work is

\[10\] days

\[12\] days

\[14\] days

\[16\] days

Let time taken by A be \[x\] days.

\[\therefore\] Time taken by \[B = 3 x\] days

According to the question,

14 / 20

Prev Next

A canal of a village can be cleaned by \[24\] villagers in \[12\] days. The number of days in which \[36\] villagers can clean the canal is

\[2\] days

\[4\] days

\[6\] days

\[8\] days

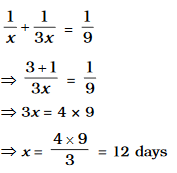
\[M_1D_1=M_2D_2\]

\[\Rightarrow 24\times 12=36\times D_2\]

\[\Rightarrow D_2=\frac{24\times 12}{36}\]

\[=8\]

Hence, The number of days in which \[36\] villagers can clean the canal is \[8\] days.

15 / 20

Prev Next

If \[35\] men can finish a piece of work in \[8\] days, then the number of men who can do the same work in \[10\] days is :

\[24\]

\[26\]

\[28\]

\[30\]

\[M_1D_1=M_2D_2\]

\[\Rightarrow 35\times 8=M_2\times 10\]

\[\Rightarrow M_2=\frac{35\times 8}{10}\]

\[=28\] men.

16 / 20

Prev Next

A can do a piece of work in \[12\] days and B can do it in \[18\] days. They work together for \[2\] days and then A leaves. How long will B take to finish the remaining work ?

\[10\] days

\[11\] days

\[12\] days

\[13\] days

17 / 20

Prev Next

A can finish a work in \[18\] days and B can do the same work in \[5\] days. B worked for \[10\] days and left the job. In how many days, A alone can finish the remaining work?

\[2\] days

\[4\] days

\[6\] days

\[8\] days

Work done by B in \[10\] days \[= \frac{10}{15} =\frac{2}{3}\]

Remaining work \[= 1-\frac{2}{3}=\frac{1}{3}\]

\[\therefore\] Time taken by A to complete the work \[= \frac{1}{3}\times18 = 6\] days

18 / 20

Prev Next

Some staff promised to do a job in \[18\] days, but \[6\] of them went on leave. So the remaining men took \[20\] days to complete the job. How many men were there originally ?

\[30\]

\[40\]

\[50\]

\[60\]

Number of men originally \[= x \ (let)\]

\[\therefore M_1 D_1 = M_2 D_2\]

\[\implies x × 18 = ( x – 6) × 20\]

\[\implies x × 9 = ( x – 6) × 10 = 10 x – 60\]

\[\implies 10 x – 9 x = 60\]

\[\implies x = 60 \ men\]

19 / 20

Prev Next

A certain number of men can do a piece of work in \[40\] days. If there were \[45\] men more the work could have been finished in \[25\] days. Find the original number of men employed in the work.

\[60\]

\[65\]

\[70\]

\[75\]

Original number of men = \[x \ (let)\]

\[\therefore M_1 D_1 = M_2 D_2\]

\[\implies x × 40 = ( x + 45) × 25\]

\[\implies 8 x = ( x + 45) × 5\]

\[\implies 8 x = 5 x + 225\]

\[\implies 8 x – 5 x = 225\]

\[\implies 3 x = 225\]

\[\implies x = \frac{225}{3}\]

\[= 75 \ men\]

20 / 20

\[5\] men can do a piece of work in \[6\] days while \[10\] women can do it in \[5\] days. In how many days can \[5\] women and \[3\] men do it ?

\[2\] days

\[3\] days

\[4\] days

\[5\] days

\[5 × 6\] men \[= 10 × 5\] women

\[\implies 3\] men \[= 5\] women

\[\therefore 5\] women \[+ 3\] men \[= 6\] men

\[\because 5\] men complete the work in \[6\] days

\[\therefore 6\] men will complete the work in \[\frac{5}{6}\times6\]

\[= 5 \ days\]