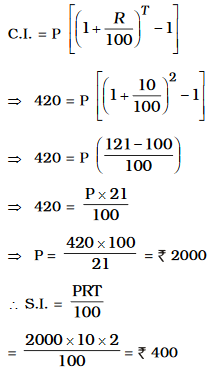The compound interest on \[Rs.2000\] in \[2\] years if the rate of interest is \[4\%\] per annum for the first year and \[3\%\] per annum for the second year, will be
\[Rs.134.50\]
\[Rs.140.50\]
\[Rs.142.40\]
\[Rs.145.60\]
Amount
\[=2000\left(1+\frac{4}{100}\right)\left(1+\frac{3}{100}\right)\]
\[= 2000 ×1.04 ×1.03 = 2142.40\]
\[\therefore CI = Rs.(2142.40 – 2000)\]
\[= Rs.142.40\]
An amount of \[Rs.6,000\] lent at \[5\%\] per annum compound interest for \[2\] years will become
\[Rs.6000\]
\[Rs.6115\]
\[Rs.6150\]
\[Rs.6175\]
\[A=P\left(1+\frac{R}{100}\right)^T\]
\[=6000\left(1+\frac{5}{100}\right)^2\]
\[=6000\times \frac{21}{20}\times \frac{21}{20}\]
\[=Rs.6615\]
The simple interest and compound interest (compounded annually) on a certain sum of money with a given rate for a period of \[2\] years are \[Rs.900\] and \[Rs.954\] respectively. The sum of money is
\[Rs.3750\]
\[Rs.4950\]
\[Rs.2690\]
\[Rs.8970\]
Difference of CI and SI for two years

A sum of money doubles itself in \[4\] years at compound interest. It will amount to \[8\] times itself at the same rate of interest in :
\[10\] years
\[12\] years
\[14\] years
\[16\] years
A sum of \[x\] becomes \[2x\] in \[4\] years.
Similarly, \[2x\] will become \[2 × 2 x = 4x\] in next \[4\] years and
\[4x\] will become \[2 × 4x = 8x\] in yet another \[4\] years.
So, the total time \[= 4 + 4 + 4 = 12\] years